
A különböző utak egyszer csak találkoznak valahol - azaz mindennek köze van minden máshoz, még akkor is ha néha ez nehezen érzékelhető. Reméljük az eddigiekből is kiderült milyen közel állnak humán is informatikai területek: támogatják és kiegészítik egymást. De mi köze az Origaminak az Imagine-hez, azaz a LOGO-hoz? Sokféle megközelítésben is lehetne közük egymáshoz, hiszen mindkettő geometriai elveken alapul és algoritmikus jellegű. De itt most nem azt vizsgáljuk miben egyformák, hanem azt: hogyan egészíthetik ki egymást a kreativitás ösvényén.
A tárgyalás fő témája a rekurzió, melynek fejlesztését két területen követjük párhuzamosan: a programozásban és Origami vágási tervek létrehozásában. Ugyan azokat a mintákat két különböző megközelítésből nézve, talán mindkettő megközelítését jobban megérthetjük és így szabad teret enged további kreatív kísérletezéseinkhez. Ugyanakkor az Origami négyzetből való kiindulása jó alapot adhat a minták elemi egységéhez és azok programozással történő továbbfejlesztéséhez. Míg a kialakult vágási minták kreatív megfontolási ötleteket adhatnak a hajtogatások mondanivalójához, teljes mértékben megmozgatva a fantáziát Használjuk a megrajzolt NÉGYZET-eket vágási tervekként, és hajtogassunk segítségükkel kreatív kompozíciókat!
Akinek először némi Origami alapokra van szüksége, az gyakorolja a különböző hajtogatásokat.
"Négyzettől a száz darumadárig"

Az indíttatás
Néhány évvel ezelőtt Japánban éltem, így alkalmam nyílt megismerkedni a japán kultúrával, nyelvvel és az emberekkel. Ezek nagyon szoros kölcsönhatásban állnak egymással, így ahhoz, hogy az egyik területet közülük megértsünk, a többi megismerése is szükséges. Az emberek és gondolkodásuk megismerése a japán nyelv megtanulásán keresztül lehetséges. A nyelv szépsége a kalligráfia csodálatát, a "sumi-e" felfedezését vonja maga után. (A sumi-e egy japán művészeti ág, mely fekete tintával való festésen alapul.) Ennek elsajátításához meg kell ismerni a papír tulajdonságait és viselkedését, így jutunk a papír megérintéséhez, hajtogatásához, és egyben egy másik művészi kifejező eszközhöz, az Origamihoz. Mindig nagyra becsültem a művészeteket, s különösen szerettem a kézműves tevékenységeket saját magam is kipróbálni. Az Origami az önkifejezés örömét nyújtja, ez vezetett efelé az ősi művészet felé irányuló kutatásaimhoz. Mint régi LOGO-s, gyakran figyelem a körülvevő világot a Teknőc szemével. Sokat tanulhatunk a természetről a fraktálokkal való játszadozásaink során, de ez a folyamat fordítva is igaz [1]. A rekurzív eljárások által létrehozott minták [2] Origami vágási struktúrákként való felhasználásának módját a következőkben ismertetem.
Párhuzamok
Legyen kiinduló pontunk az az egyszerű eljárás, melyet minden kezdő megvalósít a LOGO-val való ismerkedése során.
 |
ELJÁRÁS NÉGYZET
:MÉRET ISMÉTLÉS 4 [ELŐRE :MÉRET JOBBRA 90] VÉGE NÉGYZET 100 |
 |
Eredményként egy 100 egység oldalhosszúságú négyezetet kapunk, mely egy olyan méretű papírt ábrázolhat, ami bármely Origami objektum kiindulópontja lehet. |
Egy háromdimenziós Origami-mű létrehozása gyerekjáték, melyben a japán gyerekek igazán tehetségesek. Sok objektum a jól ismert alaphajtogatások körébe tartozik, míg a továbbiak a képzelet és tehetség függvényeiként születnek meg. Az Origami leghíresebb alapműve valószínűleg a daru vagy "tsuru", ami Japánban szerencse-madárként tisztelt állat. Lássuk tehát a daru alaphajtogatási vonalait:
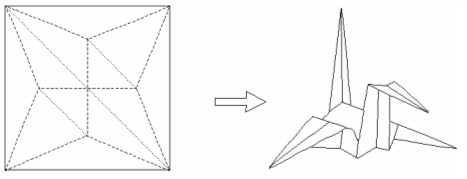
...de a befejezés már a művészi szemlélettől függ. Amint Kunihiko Kasahara, kedvenc Origami-művészem könyvében olvasható [3]:
"Az elszánt Origamizó számára ez a vonzalom tárgya, s egyben a kihívás szellemének ösztönzője is."
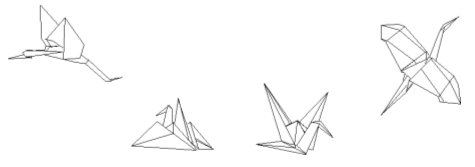
Akira Yoshizawa[4] Toshio Chino[5] Jun Maekawa[6] Kunihiko Kasahara[3] hajtogatási variációi, de érdemes megnézni Eiji Nakamura további munkáit is [7].
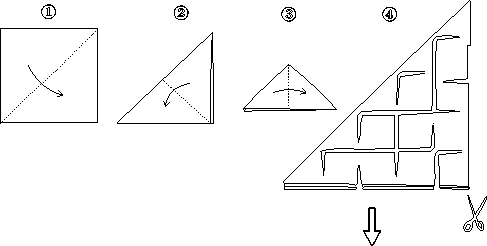
Az első vágások - az első NÉGYZET
Menjünk vissza a papírlapunkhoz, vagy más néven NÉGYZET-ünkhöz. Felezzük meg oldalait, és vágjuk be a hajtási vonalak mentén majdnem teljesen a közepéig. Ezt a vágási folyamatot a Teknőccel is elvégeztethetjük az ELŐRE :MÉRET utasítást a következő algoritmussal helyettesítve:
 |
ELJÁRÁS 1OLDAL
:MÉRET ELŐRE :MÉRET / 2 JOBBRA 90 ELŐRE :MÉRET / 2 BALRA 180 ELŐRE :MÉRET / 2 JOBBRA 90 ELŐRE :MÉRET / 2 VÉGE |
Megjegyzés: matematikai érdeklődésűek kedvéért: ez egy általános Koch-görbe eljárás [8] , ahol N=4 (az oldalak száma) és r=1/2 (a fokbeosztás aránya).
Írjuk meg az 1OLDAL eljárást felhasználó 1NÉGYZET eljárást.
ELJÁRÁS 1NÉGYZET :MÉRET
ISMÉTLÉS 4 [1OLDAL :MÉRET JOBBRA 90]
VÉGE
Tulajdonképpen az 1OLDAL :MÉRET helyettesíti az eredeti NÉGYZET oldalát.
 |
A most kiadott 1NÉGYZET 100 utasítás eredményeként valójában négy negyed négyzetet láthatunk, de a Teknőc által megtett utat megfigyelve kapjuk a papír kívánt határait. |
Ne vágjuk be a kapott vonalakat ténylegesen a középpontig, hagyjunk ki néhány milliméteres szakaszt, hogy a papírunk ne essen szét.
Kreatív választásunk eredményeként adódhat, hogy a daru feje melyik sarokhoz kerüljön. Kísérletezzünk bátran más vonal-vágási kombinációk kipróbálásával is. A következő oldalakon, a hagyományos japán Origami legrégebbi, "Senbazuru" (A száz daru) [9] című kéziratából származó példákat láthatunk. 1797-ben Rokouan Gido Ichien, egy kuwanai templom főpapja írta Ise-no Kuni városában. 49 féle daruhajtogatási módszert találunk benne, négyzet vagy téglalap alapú papírból kiindulva, melyen adott vágási terveket kell megvalósítani annak érdekében, hogy számos, egymáshoz kapcsolódó darukat hajtogathassunk felhasználásával. Ezen amulettekről Akizato, a "Haiku" leghíresebb költője írt verseket, hogy lírai kifejezésekkel hangsúlyozza szépségüket, és Shunsensai rajzai illusztrálják őket. (A Haiku egy 5-7-5 szótagú sorokból álló rövid verstípus, melyben a költő legmélyebb érzelmeit kísérli meg kifejezni a természet egyszerű és gyönyörű nyelven való leírásán keresztül.)
| 1.) Hullámzó
tenger
|
2.) Szélmalom
|
| 3.) Kimono
|
4.) Hópehely
|
| 5.)
Tökfilkók
|
6.) Káosz
|
| 7.)
Harangvirág
|
8.) Szelek
|
|
Megjegyzés: Az kis körök a daru fejének helyzetét jelölik. |
Japánban minden családnak van címere, melyek tartalmazhatnak ilyen Origami jelképeket is. A japán családi címerek (mon) eredete a XI. századba nyúlik vissza. Azokban az időkben az ország magasrangú személyiségei különleges textil-terveket kezdtek használni a császári udvarnál viselt hivatalos öltözetükön, amelyek a családi címereket ábrázolták [10].
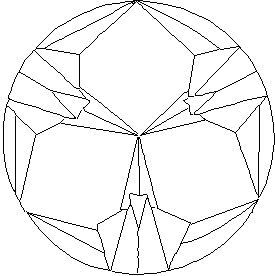
Térjünk vissza a LOGO eljáráshoz és kísérletezzünk ezzel, hogy eredményeinket felhasználva a daruk számát növelhessük. Első lépésként, annak érdekében, hogy valóban az aktuális vágási felületet lássuk, helyettesítsük az 1OLDAL eljárást egy szemléletesebb ábrát készítő eljárással, amelyen könnyebben lehet kivenni a vágási vonalakat és a papír összekapcsolódási pontjait:
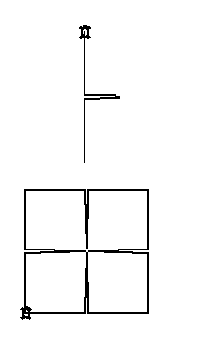 |
ELJÁRÁS OLDAL1 :MÉRET
ELJÁRÁS NÉGYZET1 :MÉRET
|
NÉGYZET1 100
A fenti eljárást a NÉGYZET1 eljárás elemeként felhasználva lehetővé teszi annak ábrázolását, hogyan és hol kell elvágni a papírt, illetve a vágási vonalakon haladva megkaphatjuk az adott szintű LOGO eljárást.
Megjegyzés: OLDAL1 eljárást egy alap vonalrajzoló eljárásnak kell tekinteni, így a NÉGYZET1-en belüli felhasználásakor az alap négyzetrajzolást adja meg.
A második vágási szint - a NÉGYZET második szintje
A rekurzió folyamatát nem könnyű megérteni, de a papírvágási technika segítségével egyszerűbbé tehető. Kezdjük el a kapott négyzeteket ismét a felezőponton bevágni, mint az előbb, negyedelve a négyzeteket, megkapva a következő szintek alapját. Ugyanekkor próbáljuk meg végiggondolni ennek algoritmikus megfogalmazását is:
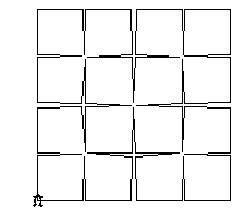 |
ELJÁRÁS OLDAL2 :MÉRET OLDAL1 :MÉRET / 2 JOBBRA 88 OLDAL1 :MÉRET / 2 BALRA 176 OLDAL1 :MÉRET / 2 JOBBRA 88 OLDAL1 :MÉRET / 2 VÉGE |
ELJÁRÁS NÉGYZET2 :MÉRET ISMÉTLÉS 4 [OLDAL2 :MÉRET JOBBRA 90] VÉGE |
NÉGYZET2 100
Ez a vágási tervek új szintjét hozza létre. Folytassuk a kivágást és az algoritmus írását a következő szinten...
További vágások - a NÉGYZET általános szintje
Megjegyzés: Fontos, hogy minden lépésben végigkövessük a vágási vonalakat, hiszen pontosan ez adja meg a Teknőc útvonalát a rajzolásban!
Mivel minden egyes vágási szintet az előző szint befejezése után végzünk el, a hozzájuk tartozó eljárásokat egymásba ágyazhatjuk, így az algoritmust addig folytathatjuk, míg a 0. szintet, az alapszintet el nem érjük, ami egy egyenes vonal rajzolását végzi:
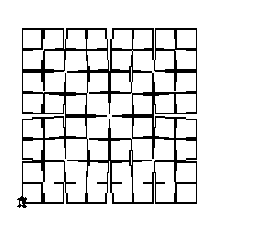 |
ELJÁRÁS OLDALAK :MÉRET :SZINT HA :SZINT = 0 [ ELŐRE :MÉRET STOP] OLDALAK :MÉRET / 2 :SZINT - 1 JOBBRA 88 OLDALAK :MÉRET / 2 :SZINT - 1 BALRA 176 OLDALAK :MÉRET / 2 :SZINT - 1 JOBBRA 88 OLDALAK :MÉRET / 2 :SZINT - 1 VÉGE |
ELJÁRÁS NÉGYZETEK :MÉRET :SZINT ISMÉTLÉS 4 [OLDALAK :MÉRET :SZINT JOBBRA 90] VÉGE |
Próbáljuk a ki a négyzetek ezen új, rekurzív eljárását és határozzuk meg a vágás szintjét. Láthatjuk, hogy a:
NÉGYZETEK 100 1
NÉGYZETEK 100 2
NÉGYZETEK 100 3
utasítások tökéletesen működnek.
Minden origami-művet egyetlen papírlapból kell létrehozni, így a vágások elvégzése közben gondosan figyeljünk arra, hogy a papír egyben maradjon. Ha ezzel végeztünk, akkor következik a feladat nehezebb része, a daruk hajtogatása úgy, hogy a papírt nem tépjük el.
Türelemmel és precizitással célba érünk!
A fej illetve farok sarkának meghatározása és a vágási terv kiválasztása egyaránt növeli a mű variációinak lehetséges számát.
Ezen az oldalon egy Rokouantól származó gyönyörű példa
leírása található meg, melynek neve: "Hyakkaku"
![]() (A száz daru).
Valójában csak 97 daru hajtogatása vihető véghez, de maga az
alap 100 egységnégyzetből áll.
(A száz daru).
Valójában csak 97 daru hajtogatása vihető véghez, de maga az
alap 100 egységnégyzetből áll.
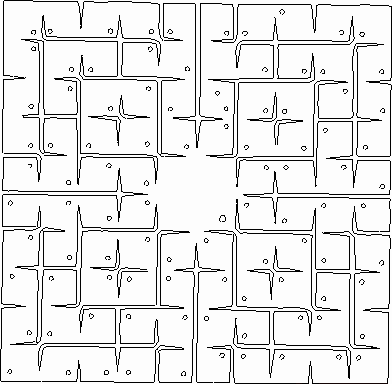
 |
100 daru
Asahina
címere |
A Haikut, melyet e csodálatos Origami ihletett nem igazán lehet lefordítani, de biztosan érezni rajta az erő kifejeződését. Valójában az "Asahina" egy összetett értelmű szó, ami egyaránt lehet hely, család vagy címer neve.
Néhány egyszerűbb variáció kipróbálása illetve sikeres befejezése során némi szakértelmet szerezhetünk ezen a területen. De meg kell, hogy mondjam, bár Rokouan könyve valóban nagy népszerűségnek örvend, a legtöbb csodáló megmarad ezen a szinten, és csak egy-két igazán kitartó személy jut el a könyv végéig. Ha a papír egy darabban való tartása akadályozza a mű elkészülését, próbáljuk meg a terv megvalósítását különálló lapokból. Úgy gondolom, ezzel nem sértjük meg Rokouan szellemét.
A fraktálok vizsgálata során olyan ismereteket szerzünk, melyeket a természetben, vagy egyéb tudományokban is felismerhetünk. Az Origamival való kísérletezés feltárja azt a tényt, hogy a tervek erősen geometrikus formákon alapulnak. Remélem, hogy a fentiek meggyőzően támasztották alá a LOGO és az ORIGAMI egymást kiegészítő kapcsolatát, amely lehetővé teszi, hogy a digitális kód, immár a képernyőt elhagyva szárnyakat kapjon a 3. dimenzió művészi kifejezésében.
Ez a fejezet, mint egy ráadás az előző fejezetek különváló építményeihez, a nagy összetalálkozásokból egyetlen egyre szándékozott rávilágítani, ezzel inspirálva az olvasót további kutatások és kísérletezések végzésére. Reméljük, hogy a tananyag különböző szemléletű megközelítései valamilyen oldalról valóban felkeltették az érdeklődést a digitális írásbeliség szerteágazó szövevényes lehetőségeiről.
Referenciák
Szerzők:
A szöveg, az illusztrációk és a mikrovilágok Turcsányiné Szabó Márta munkái.
Márta Turcsányi-Szabó, “From SQUARE to a thousand cranes”, in Proceedings of the Fourth European Logo Conference, pp.145-151., University of Athens, Department of Informatics, Athens Greece, 1993. http://comlogo.web.elte.hu/team/publikaciok/elogo931.html
[1] Benoit Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman and Co., San Francisco, 1977.
[2] Clayson, J. Visual Modelling with Logo - A Structural Approach to Seeing, MIT Press, 1988.
[3] Kunihiko Kasahara, Origami Omnibus, Japan Publications Inc., 1988.
[4] Akira Yoshizawa, Origami Toku Hon II (Origami tanulmányok II), Kamakura Shobou Publications, 1986.
[5] Kunihiko Kasahara, Origami Shinseki (Az Origami új korszaka) of Viva Origami series,
Sanrio Publications, 1989.
[6] Jun Maekawa, Kunihiko Kasahara, Viva Origami, Sanrio Pblications, 1983.
[7] Eiji Nakamura, Henka Orizuru (Daru Origami variációk), 1971.
[8] Benoit Mandelbrot, Fractals form, chance, and dimension, W. H. Freeman and Co., San Francisco, 1977.
[9] Rokouan, Akizato, Shunsensai, Sembazuru (Az ezer daru), 1797. http://www.origami.gr.jp/Model/Senbazuru/index-e.html
[10] Compiled by the Matsuya piece-goods store, Japanese Design Motifs, Translated by Fumie Adachi,
Dover Publications Inc., 1972.
További címerek találhatóak: http://ccins.camosun.bc.ca/~jbritton/jbkamon.htm