|
Secondary Maths tools |
By Katarzyna Oledzka OEIiZK-PL

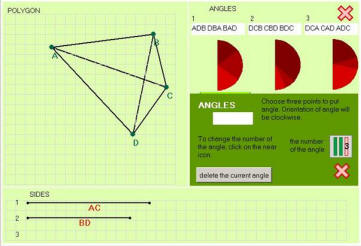
The program supports investigations and discovering properties of polygons'. Student can build his or her own figure and check its properties. Especially he or she can compare the length of segments, measure the angles and also illustrate the periphery and area.
To draw a polygon student have to define consecutive points which build the figure. Next he/she can analyse the properties of the polygon. He/she can add a free point on the pane or a point attached to a segment either a point dividing the segment into half or any point of segment. Moreover for each point one can find its project on a segment. In the case of a triangle this allows constructing heights and medians.
With this application student can compare segments on three levels – it can be dependent of side’s length or diagonal’s length or polygon’s periphery. Similarly he/she can compare angles on three groups, both analyse sum of angles or compare measures between angles.
After choosing the "area" option allows to find out how the area changes while resizing the figure. How some measurements affect the area.
Moreover there are some questions for students with possibility to evaluation and expand.
Material can be divided into three groups –triangle’s properties, problems with quadrilateral and other properties of polygons.
For the first group the subjects are:
For quadrilateral we have properties:
For third group you can examine dependence on number of sides, vertexes and diagonals and other properties connected to area and periphery.
The best way of using the program are classroom group activities.
See:
How to translate polygons
See: Polygons in Slovak and
Polish version
Authors: Witold Kranas, Andrzej Walat

The microworld Vectors is comprised of two parts in fact two smaller microworlds dedicated to vectors in mathematics and physics.
The aim of the mathematical part is to help students to get a comprehensive insight of a notion of vector, to learn a variety of vectors representations and applications. The exercises are aimed to help the student to build connections between analytical and graphical vector representations.
The aim of the second part is to introduce vectors in physics and to analyze the role of velocity and force (acceleration) vectors. It helps to understand how force is changing velocity vector and thus how force rules the body movement (second Newton's Law). The microworld could be named "Movement Laboratory". It contains 2 important examples: body movement in uniform gravitational field - near the Earth surface - enables to analyze different kinds of "shots" and body movement in central gravitational field, for example satellite or planetoid movement. The example of steering the body movement on a round track gives the possibility to understand the role of centripetal force.
In both parts the exercises are have "open" character. There are possibilities of different kinds of activity, gathering the experience, answering questions: what will happen when we change...?
The microworld is suitable for both classroom activities (in secondary school) and home learning.
See:
How to translate vectors
See: Vectors in Hungarian,
Slovak and Polish
version
Author: Andrzej Walat

The microworld Visual modeling with Imagine Logo is comprised of the exercise book for a student and a set of small Imagine projects – the solutions of some problems from the book. Initially it may seem to be a book about creating graphics in Logo – and in some senses it is. But the main aims of the book are to help student became a good problem solver, to improve his understanding of mathematics and to increase his confidence in using various mathematical ideas in the context of interesting art and design activities.
The book contains 16 activities. Each activity starts with an example and/or short explanation, which is followed by 1 to 4 problems. In addition, the book contains solutions for all the problems, together with tips and comments.
The set of 16 activities can be regarded as a resource for various mathematical assignments. The various problem scenarios require the application of a number of mathematical ideas such as: discovering relationships between measures of different elements of geometrical shapes and representing them in the form of equations, solving equations, estimating by the trial and error approach, using trigonometric functions and so on. The student usually has to join a number of observations and facts together to get the solution to the problem. The mathematical problems are posed in a kind of a disguise. The student isn’t told that he should use an equation or any particular formula or trigonometric function. He isn’t even told that he should use any mathematical knowledge at all. Usually there are many ways of using mathematics to solve the problem. It is up to the student which mathematical idea he will choose so he learns to become an independent problem solver
Apart of equations and trigonometric function which are used and discussed openly, there are other very important mathematical ideas which are incorporated but not in an explicit way. The first of them is recursion. We use recursion from the very beginning. But we don’t use the word recursion. Why not? Because we strongly believe in the idea of indirect teaching. People can learn powerful ideas without being deliberately taught. Even beginners in programming can fully understand simple procedures without studying the “grammar” of recursive constructions, just on the basis of understanding the task. Further more - they are able to create similar constructions themselves. To understand the procedure you need nothing more but an understanding of the task and natural language. Learning recursion may be like learning a language without being taught the grammar beforehand. Of course there is nothing wrong if the teacher organizes a discussion about recursion on the basis of known and understandable examples.
The other powerful idea is randomness. The solutions use plenty of expressions like ANY or 5 + RANDOM 11 or even [-100 –100] + RANDOM [201 201]` which return random values. Many pictures in the book were generated randomly. It was not our intention to study random events seriously. It is the main aim of another of our microworlds “Laboratory of Randomness”. But it was definitely one of our aims to get the students to feel the power of randomness.
Research has revealed that many weak pupils hold beliefs about mathematics and mathematical learning, teaching and problem solving such as the following. :
- Mathematical problems have one and only one right answer.
- There is only one correct way to solve any mathematical problem; usually the rule the teacher has most recently demonstrated in the class.
- Ordinary students cannot solve mathematical problems by themselves.
- Solving a mathematical problem should not take more than five minutes.
- Being able to solve a mathematical problem is merely a question of luck.
- The mathematics learned in school has little or nothing to do with the real world.
There is evidence that these beliefs exert a powerful influence on students’ willingness to engage in mathematical problems, on the kind of activities they perform when confronted with a mathematical problem, on the kind of knowledge that they are inclined to use during their problem-solving attempts, and on the way they evaluate their success or failure to solve problems. (De Corte et al., 1997)
The project is intended to provide a remedy to these beliefs. The author hopes that both the teacher and the student will notice and appreciate the effort made to give the impression that almost each problem has a infinite number of different solutions and that: being able to solve a mathematical problem is a not mere a question of luck – “you will find at least one solution if you give yourself enough time”.
The structure and content of the microworld (Visual modelling with Imagine Logo) was carefully designed to help an individual learner – the student of the upper secondary school – to learn independently. The first of the two main parts of the exercise book– is comprised of 16 activities. Each activity is usually short – from 1 to maximum 3 pages – and can serve as a worksheet for a student.
The second of the main parts of the book contains hints and solutions. It is designed to serve as a scaffolding for a student. In the case of being in stuck the student can find the appropriate support in the solution part.
Though independent individual learning with Visual modeling with Imagine Logo is absolutely possible and – we hope – should be interesting and efficient the group learning is much better for many reasons, mainly because:
- working together in pairs or triples– particularly running the Imagine projects and observing random processes – stimulates discussion of a great educational value,
- a best scaffolding for a learner – particularly in a case of being in stuck – is other learner,
- majority of problems have open character, they have a variety of good solutions, working in a group gives the opportunity to compare and discuss various ways of managing the problem.
The microworld Visual modeling with Imagine Logo is suitable both for creative classroom and home learning activities.
See: Visual modelling in Hungarian Live web site, Slovak, English, Polish version
Author: Andrzej Walat
The randomness is one of the most powerful ideas and has great practical importance. On the other hand it seems to be extremely difficult. Let us quote Nassim Taleb – a professor at the Courant Institute of Mathematical Sciences of New York University and a renowned trader: “our mind is not equipped with the adequate hardware to handle probabilities” and “most results in probability are entirely counterintuitive”. The basic notions like random variable, probability distribution, expected value seem to be high above the level of the average high school student. Even if he/she is capable of computing he/she often does’t understand probability. It is because of the traditional very formal and abstract way of introducing probability.
It is the role of learning microworlds to turn abstract ideas into observable facts and support a variety of activities that provide straightforward access to deep ideas by working with objects. The learning microworld - Laboratory of Randomness is build of the book and a number of Logo projects attached on the CD. Each of these project is a kind of learning micro-microworld which provides the student with an opportunity to observe and examine various facets of randomness (like important characteristics of random variables) without – and long before – introducing any formal definitions. This attempt is not against formalism. On the contrary. The main goal is to help the student in harnessing formalism, making it understandable and handy. And to develop the need for formalism.
The role of the computer and in particular the Imagine Logo environment is great. The computer is indispensable as a toll capable of generating a million sample path per minute. The Imagine Logo is used as an environment of developing a variety of learning microworlds and a language which allows us to represent and explore deep ideas. The student can build and explore two kinds of models of random processes: the realistic and abstract ones. The role of the first category is to help students to understand problems, main questions and deep ideas involved. The role of the second category is to help find solutions. Both categories are equally important.
The book starts with a number of relatively easy examples and problems. The student will examine mainly the first category of models the realistic ones and only very simple abstract ones. The main goal is to give a student the feeling of randomness. Gradually the ratio of the two kinds of models changes. The proportion of abstract models grows. We use formal representations more often. Apart from traditional representations like mathematical equations we introduce other new tools of expressing ideas: the formal definitions of procedures in Logo. These definitions are usually very short and simple, but this doesn’t mean easy. They may be regarded as difficult both to understand and to build. It is mainly because they are an absolutely new kind of language and mastering each new language takes time and effort. The question: “Why?” is not only quite natural but inevitable The answer is: because …
…there are actually a vast range of abstract systems based on simple programs that traditional mathematics has never considered. And because these systems are in many ways simpler in construction than most traditional systems in mathematics it is possible with appropriate methods in effect to go farther in investigating them.
Stephen Wolfram: The new kind of science.
We strongly believe that randomness is that range of interest that we can explore and understand much deeper owing to these new means of expressing mathematical ideas like formal definitions of procedures in Logo.
The author believes in the main principle of Logo community: No threshold and no ceiling. He regards both parts of this principle equally important. So he starts from the relatively easy but not trivial problems, because there should be no thresholds. But he doesn’t hesitate to introduce some really hard but interesting problems at the end of the book. Logo is not a childish tool for small children. It is a very powerful and useful tool of investigating advanced topics and solving hard problems.
The structure and content of the microworld (Laboratory of randomness) was carefully designed to help an individual learner – the student of the upper secondary school – to learn independently. The first of the two main parts of the exercise book– is comprised of 17 units. Each unit is usually short – from 1 to maximum 3 pages – and can serve as a worksheet for a student. There is a small Imagine project connected with each unit. There are 14 projects altogether on attached CD.
The second of the main parts of the book contains hints and solutions. It is designed to serve as a scaffolding for a student. In the case of being in stuck the student can find the appropriate support in the solution part.
Though independent individual learning with Laboratory of Randomness is absolutely possible and – we hope – should be interesting and efficient the group learning is much better for many reasons, mainly because:
- working together in pairs or triples– particularly running the Imagine projects and observing random processes – stimulates discussion of a great educational value,
- a best scaffolding for a learner – particularly in a case of being in stuck – is other learner,
- majority of problems have open character, they have a variety of good solutions, working in a group gives the opportunity to compare and discuss various ways of managing the problem.
The main locus of use the Laboratory of Randomness we can foreseen for a nearest future is an extra classroom activity. It may be also suitable for classroom activities in upper secondary school but generally requires dedicated teacher and students because the mathematical content is rather advanced and compelling. The chosen parts, like simple simulation projects and related materials may be used with the average students.
Author: Andrzej Walat

Many people (particularly many young people) like to play. This activity book together with a variety of projects on attached CD gives the student the opportunity to play the games, to discover their rules, and to learn how to create them. While playing the games and creating them he/she will discover and learn a good deal of hard mathematics. Almost each game contain some mathematics. It is the case off all games described in the book. Some people who don’t like mathematics, they have learned at school, don’t have any objections against the mathematics of games. Very often mathematics that seemed to be boring and meaningless appears to be very attractive and useful in a new context. In this book the student will see and learn a part of linear algebra in a new context of computer games. The sets of simultaneous linear equations have great practical applications and were always the important part of school curricula. But they were practically unmanageable if you had only a pencil and paper at your disposal. The situation is absolutely different if you have a computer with appropriate environment like Imagine Logo. An operating on the sets of equations, matrices of coefficients and vectors of solutions may became an interesting and funny activity.
The book contains 10 units and appendix. Usually each unit begins from introducing a game. Next the student is asked to answer the questions and/or solve problems. Some problems are only the starting points for further activities and full solutions will be given in the following units. Some solutions are fully described and explained in the last part of the book – Solutions.
The first part of the book is the set of 10 activities which can be used by individual student as a kind of worksheet supported by Imagine projects attached on CD. that can help to understand the
The structure and content of the microworld (Algebra of Games) was carefully designed to help an individual learner – the student of the upper secondary school – to learn independently. The first of the two main parts of the exercise book– is comprised of 10 units/activities. Each activity is usually short – from 1 to maximum 3 pages – and can serve as a worksheet for a student. There is a small Imagine project connected with each unit.
The second of the main parts of the book contains hints and solutions. It is designed to serve as a scaffolding for a student. In the case of being in stuck the student can find the appropriate support in the solution part.
Though independent individual learning with the Algebra of Games is absolutely possible and – we hope – should be interesting and efficient the group learning is much better for many reasons, mainly because:
- working together in pairs or triples– particularly running the Imagine projects and observing random processes – stimulates discussion of a great educational value,
- a best scaffolding for a learner – particularly in a case of being in stuck – is other learner,
- majority of problems have open character, they have a variety of good solutions, working in a group gives the opportunity to compare and discuss various ways of managing the problem.
The main locus of use the Algebra of Games we can foreseen for a nearest future is an extra classroom activity. It may be also suitable for classroom activities in upper secondary school but generally requires dedicated teacher and students because the mathematical content is rather advanced and compelling.